Antwerp QC, Much of Belgian Core, Leaves Competitive Quidditch
Criticism is a common refrain to any quidditch volunteer. Since its founding, the quidditch community has been populated by a wide array of passionate participants–and their passion has led them to be ever vigilant in giving feedback to the people running and organizing the sport they love. That feedback can range from constructive to downright abusive and from valid to absolutely inane, and its presence can make volunteering at any level of this sport as demoralizing as it is gratifying.
Since 2011, one volunteer has been integrally involved in the inner-functions of the sport, ensuring that each season ran as smoothly as possible, while staying unnoticed by the vast majority of players. Yet, in that same time period, no volunteer has been criticized more than this one, and almost always for reasons completely out of their control and by people with little-to-no understanding of everything they do. This “volunteer” is none other than the USQ Standings Algorithm, and probably no standing USQ policy has been more unwavering nor more maligned in its nearly nine-year history.
The USQ Standings Algorithm was first created in 2011 under the purview of the League Management Council (LMC)–the precursor to USQ’s gameplay team–to create some way of ranking teams in the runup to IQA World Cup V. This process, led by Will Hack and spearheaded by Kevin Oelze and Alex Clark, developed the precursor to the standings algorithm used today in a little under two months, doing its best to seed the 60 Division I and 25 Division II teams into pools for that tournament. Thanks, in part, to the limited amount of game information coming into the tournament and, in part, to its novelty, the standings produced their fair share of duds–placing the first and second seed-receiving University of Texas and University of Florida at 34th and 23rd overall, respectively, while putting University of Rochester (0-4 finish) and Ives Pond Q.C. (1-3 finish) as pot one teams. Generally, however, that standings format showed promise and, for the first time in league history, gave an objective system for determining team seeding from a messy assembly of teams scattered across the country playing a varying amount of games per season.
With over a year in between IQA World Cups V and VI, the LMC–renamed the IQA Gameplay Team–set to improve the standings formula by adding a strength of schedule adjustment, a minimum game requirement and increasing the overall algorithm transparency. That new algorithm underwent a few cosmetic changes before the IQA World Cup VII season, and has remained unchanged ever since. For an algorithm that was brainstormed in two months; has only had one major and one minor overhaul since then; and has remained essentially unchanged since Middlebury College was the reigning national champion, it is certainly valid to wonder about its robustness and reliability. These days, with online complaints about the algorithm seeming to be an annual tradition, a casual observer might certainly take on the opinion that the algorithm is horrendously out of date. That said, the algorithm is likely one of the sturdiest policies to come out of USQ, and the fact that it has lasted longer than USQ has been an official organization is an indication of its strength–not its weaknesses.
To address some of the formula’s main critiques, it would be important to know what pieces go into the algorithm itself (if you don’t care at all about the math, feel free to skip this paragraph). Firstly, the formula generates a “SWIM” value (for Snitch When It Matters–an awkward backronym developed by Oelze who recalls that the LMC wanted to spell out that word but can no longer remember why). The term has led to minor confusion as it has now become a colloquial definition of a team’s seeking performance during in-range games. In the ranking formula, however, SWIM essentially serves as a quidditch-based stand-in for how impressive a team’s margin of victory is. Winning quaffle point margins scale linearly until a team is winning by 80 points or more, and above that increase by a decreasing rate. Snitch catches by the winning team always boost the SWIM rating they get for that game, and help more when the game ended “in range.” Snitch catches by the losing team never affect the SWIM rating. That SWIM rating (positive for wins and negative for losses) is then averaged for every game a team plays in a season, and then all SWIM ratings are scaled to ensure that all teams have a non-negative SWIM rating. After this, that rating is multiplied by their win percentage, scaled to run between 50 and 100 percent in order to mitigate the penalty teams that play an excessively difficult schedule would otherwise take from a flat win percentage multiplier. Since a team’s SWIM rating and win percentage run the risk of being unnaturally inflated if that team plays a too-easy schedule, a strength of schedule multiplier is added to the formula to help adjust against teams which attempt to pad their schedule with an excess of games against easy teams. A multiplier is also added to penalize teams that haven’t played a certain amount of games, but due to USQ policy changes, this multiplier is no longer practically used for any standings-based seeding purposes.
Despite seeming complex, the formula is actually remarkably clean when observed from a birds-eye view: margin of victory multiplied by win percentage multiplied by strength of schedule–and all scaled to an optimized level for comparing a league’s worth of teams situated across the country. This has created a system that has done an impressive job at estimating a team’s true quality for the past seven seasons–and even more impressively done so only using data from that season. That’s not to discount that every year the formula might whiff on accurately determining a specific team’s strength, as it is generally critiqued for doing two or three times a year. But, in the meantime and in the majority, over 100 teams are relevantly sorted by a logical and fair order of team quality.
Each year, the most common standings formula complaints tend to center around “team A being overrated,” but most of these complaints are more input-based than algorithm-oriented. Generally, an overrated team tends to have played in an isolated part of the country or had a particularly easy schedule, leading to an exceptionally inflated strength of schedule in addition to a high win percentage and margin of victory. Take for example the exceptionally notorious USQ Cup 9 version of the Rain City Raptors. Playing only two teams from outside the Northwest, the squad went 14-1 and received a pot one seed at nationals, only to go 0-4 in their pool. This team was rightfully critiqued for being over-inflated in the ranking algorithm, but the only fix for equalizing the team’s ranking would have been to have them travel further and play a more-competitive regular season schedule–a feasible fix but one that a player-oriented league like USQ would be justifiably loathe to mandate. That year’s Raptors might be the worst example of the algorithm completely misrepresenting a team’s actual quality level, but the critiques surrounding the algorithm usually surround teams in very similar situations. Even the opposite can be true–albeit rarely–as demonstrated with this year’s Twin Cities Q.C. Before earning an autobid at the Hoot and Howdy Invitational, the team was at risk of missing out on a nationals berth after playing what may have been the most difficult strength of schedule in modern quidditch history. Systems like this publication’s Elo standings can generally stake a claim at being more predictive and, thus, more accurate at judging team quality. However, they receive the benefit of being able to peer into past seasons to make estimations about the quality of teams and the league as a whole–though they still remain flummoxed at judging the quality of new teams. USQ’s algorithm, for the sake of fairness to all teams, gives itself the handicap of only looking at data from the current season in making its standings. In doing so, it likely uses an optimal or as-close-to-optimal-as-feasibly-possible system within those constraints. From an Elo standings perspective, this accomplishment is astounding–Elo tends to be remarkably inaccurate when judging the quality of a new team until that team has played about a dozen games or so, and USQ’s algorithm essentially inputs more than 100 “new” teams each season and sorts them relatively efficiently by season end.
Since 2016, when The Eighth Man’s Elo Standings was released, I have received regular questions on whether USQ should use an Elo-based rating system. While an Elo-based system can certainly bring a level of increased accuracy over the system currently used, there are a couple of huge fairness issues that would arise if it were ever used for official purposes.
- Every new team needs to be given an arbitrary rating value.
In our rating system, this is broken down to new club teams receiving a new rating of 1500 and new college teams receiving a new rating of 1300. A potential USQ Elo rating system wouldn’t necessarily need to use these values, but some value would need to be set. If that rating was too high, like 1500, then it would simply make sense for every club team that finished the previous season below that level to disband and refound as a new team, thus benefiting from an artificial rating hike. If that rating was set too low, then new teams joining the league would be unnecessarily penalized and would either need to play more games per season to catch up to the rest, or face a lower likelihood of qualifying for nationals. This effect would be especially exacerbated for seeding early-season tournaments like Fall regional championships.
- Teams’ previous ratings would provide “hangovers” toward future seasons.
Even if college teams might be unable to disband and refound to juice their initial Elo standings, their previous seasons’s records could potentially have an unfair effect on how their team is rated throughout the season. For teams that rapidly improve from one season to the next–for example, Harvard University (currently 13th in college Elo, 4th in college USQ standings) or Creighton University (21st in Elo, 11th in USQ)–they would feel the “hangover” of their last season’s finish as an unfair drag on their season’s standings. The converse is just as true with perhaps even worse consequences. Teams that are riding high from last year’s finish but may have lost a significant class of seniors–see UC Berkeley (15th in Elo, 23rd in USQ)–will have their ratings overinflated by Elo standings. These teams would also have an insidious incentive against playing games–something any ranking algorithm would want to strongly avoid. Furthermore, since an Elo-based system results in teams jumping faster in rankings by beating better teams, these teams would almost certainly create a “feeding frenzy” with other teams jumping to beat up on them early in the season to take advantage of their inflated Elo standings.
Both of these are fairness issues that can be completely controlled if each season is treated as a completely new iteration, with zero information being brought from one season to the next, as USQ’s ranking system currently does. As mentioned above, however, Elo operates abhorrently in the absence of past data, and any Elo-based system that tried to compete with USQ’s standings algorithm using solely data from the current season would be blown out of the water.
But the fact that two separate ranking systems exist, each optimizing its own priority–for USQ’s, fairness, and for The Eighth Man’s, predictivity–begs the question, is there some neutral ground between the two? Is there a system that can potentially maintain at least some of the season-to-season accuracy that the Elo-based algorithm provides while providing at least most of the absolute fairness the USQ standings algorithm provides? This is a question that has nagged me for the past several months, especially as this season’s Elo algorithm updates seem to have done a lot to improve its accuracy. While I certainly don’t have an ideal answer–a league-wide rankings algorithm shouldn’t only be generated from a thought experiment–a few months worth of shower thoughts have led me to an answer that I think at least somewhat balances the issues addressed above regarding the usage of an Elo-based standings system. This hypothetical system could have the further benefit of eliminating the rare quirks of teams inflating their standings by playing a long string of blowout games against easy competition or playing in a geographic corner of the country that throws off their strength of schedules. To do so, this standing system would be at least partially based on the current Eighth Man Elo Standings, but make the following changes:
- Increase the weighting of the seasonal readjustment.
This would in some part control that a ratings hangover would drag down teams who quickly improve from one season to the next and would float teams who are bloated by previous seasons’ success. While it wouldn’t completely fix these issues, if used in conjunction with a game-minimum policy similar to the one USQ already has in place, it would serve as a decent method to increase the current level of fairness that the Elo system offers. This is a fairly easy system to play with until an optimal level is found, and this readjustment factor was actually decreased between the USQ Cup 11 and USQ Cup 12 seasons to make our algorithm more predictive. While it’s likely that such a change (say to an adjustment of 1/3 or 1/2 towards the mean) would sacrifice some of its early-season predictivity, it would still result in a system with more accuracy than an Elo system that must be freshly reset every offseason.
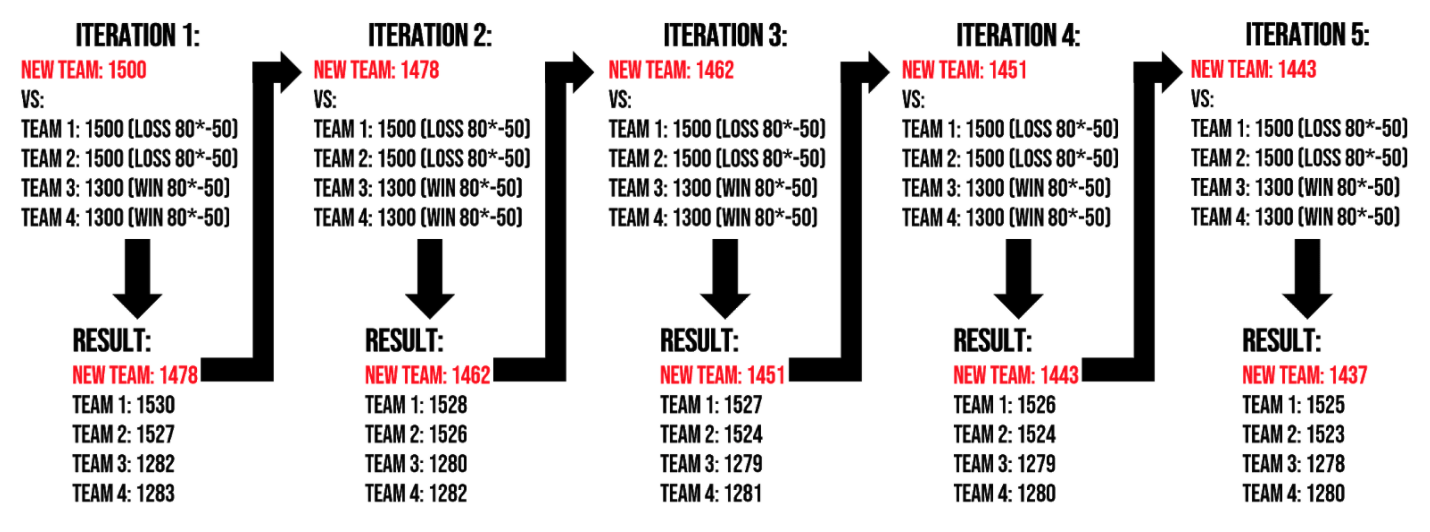
- Recursively adjust the Elo standings of each new team a set number of times.
This adjustment almost completely eliminates the problems raised above in problem one. In this system, every team would still receive an arbitrary Elo standing, but their given Elo standing would change each time they play a game. This recursive adjustment would certainly be labor intensive, but could potentially be programmed to do so automatically. In a system like this, a team would start at 1500, but after their first tournament, that initial rating would be reset to wherever their rating landed after that first weekend of games, and the season would be re-simulated and repeated X times (five times will generally give you an accurate estimate after as little as three games). For a hypothetical team playing their first tournament where they lose two game against teams with rating 1500 and then win two against two teams with rating 1350, their rating recursion would look as follows:
Iteration 1 (initial state): 1500; Iteration 2: 1478; Iteration 3: 1462; Iteration 4: 1451; Iteration 5 (and new starting Elo): 1443.
This recursion of their initial Elo standing would continue each time they played games for the rest of the season, giving a more accurate reflection of that team’s quality. This would, in theory, eliminate any benefit that a team would have of refounding as a new team to boost their Elo, while allowing new teams to legitimately rise or sink to the level they initially start at, and to not overbenefit or overpenalize opposing teams they play early in the season if their initial rating is miscalibrated. This is a change that would likely improve any Elo algorithm when optimized, but something that certainly would be more labor intensive as it would result in a team’s starting Elo rating changing every time they played additional games. Theoretically, a team’s first 10 games could be used to determine their starting Elo in this manner, thus saving some effort while maintaining an improved level of predictivity.
While it’s hard to determine exactly how much more accurate these changes would make the ranking system, even if it did turn out to be an ideal hypothetic improvement of 50-100 percent more predictive, there are certainly more value changes that would need to be factored into completely overhauling the system used for standings. As mentioned above, such a system would almost certainly sacrifice some fairness when compared to the current system, but something like “fairness” is much more subjective than determining the exact predictivity of an algorithm. This system would have parameters that could be adjusted to set its optimal position on a “fairness-accuracy continuum” but where the optimal position on that continuum lies would certainly be more of a value judgment than a objective one; any system that fell too close to the hypothetical fairness end of this continuum would probably benefit from just using the current USQ Standings Algorithm. An Elo-based system could also benefit from having an easy system for weighting college vs. college, club vs. club or college vs. club games differently, but once again the values given to those weights would likely end up being more subjective than objective.
After seeing how much the Elo algorithm has improved this season, I initially set out to write an article that was more elegiac than celebratory of the USQ Standings Algorithm, believing that it had served its time admirably but was time to be retired. The deeper that I went into the weeds, however, the less obvious that hypothesis became. There are certainly more accurate formulas that could be used for league rankings, but their implementation would come with its own subjective sacrifices in fairness and transparency. It is likely that under the current seasonal structure that no rankings algorithm–no matter how optimized– could perfectly sort teams by quality across such a wide geographical region with so few inter-regional games played. The top priority may not be to optimize a perfect standings algorithm, but instead to find regional and national tournament structures that increase the likelihood of the best teams succeeding. That’s an article for another time, but for those interested, I strongly recommend you check out my colleague, Ethan Sturm’s, article from earlier this Spring.
Kevin Oelze contributed reporting to this article.
Archives by Month:
- May 2023
- April 2023
- April 2022
- January 2021
- October 2020
- September 2020
- July 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- August 2019
- April 2019
- March 2019
- February 2019
- January 2019
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- April 2018
- March 2018
- February 2018
- January 2018
- November 2017
- October 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
Archives by Subject:
- Categories
- Awards
- College/Community Split
- Column
- Community Teams
- Countdown to Columbia
- DIY
- Drills
- Elo Rankings
- Fantasy Fantasy Tournaments
- Game & Tournament Reports
- General
- History Of
- International
- IQA World Cup
- Major League Quidditch
- March Madness
- Matches of the Decade
- Monday Water Cooler
- News
- Positional Strategy
- Press Release
- Profiles
- Quidditch Australia
- Rankings Wrap-Up
- Referees
- Rock Hill Roll Call
- Rules and Policy
- Statistic
- Strategy
- Team Management
- Team USA
- The Pitch
- The Quidditch Lens
- Top 10 College
- Top 10 Community
- Top 20
- Uncategorized
- US Quarantine Cup
- US Quidditch Cup